Introduction

Grover's algorithm is a quantum algorithm developed by Lov Grover in 1996. It is a well-known quantum search algorithm that can efficiently search an unsorted database to find a specific target item. This algorithm provides a quadratic speedup compared to classical algorithms, making it a significant result in the field of quantum computing.

Imagine you have an unsorted database with $N$ items, and you are given a promise that only one item in the database satisfies a particular condition or is marked as the "target" item. The goal is to find the target item using as few queries as possible.

Classical vs. Quantum search

In classical computing, you would need to perform an average of $N/2$ queries to find the target item in an unsorted database. However, Grover's algorithm can achieve this with only about $\sqrt{N}$ quantum queries, providing a quadratic speedup.

Breaking Symmetric Cryptosystems

Grover's algorithm could also be used to break certain cryptography methods such as Advanced Encryption Standard (AES), which is used by many (such as WinRaR). AES uses keys with a length of 128, 192 and 256 bits. With Grover’s algorithm, a 256 bit key can be found in 'only' 2128 iterations. That is still an enormous number, however it is almost 1040 times faster compared to brute forcing! If large quantum computers become available, AES users would be advised to use keys with more than 256 bits.

Public-key (RSA, DH, ECDH): Broken by Shor’s algorithm
Modes of operation (GCM,CBC-MAC) Broken by Simon’s algorithm
Block Ciphers (AES, DES): Attacks improved by Grover’s algorithm
Hash Functions (SHA2): Attaches improved by Grover’s algorithm
Password hashing (PBKDF2, scrypt): Broken by Grover’s algorithm

How it works

Grovers Algorithm

Start with state $|0\rangle$
Apply $H^{\otimes n}$
Repeat $\sqrt{2^n}$ times
- 3a. Apply phase inversion operation: $U_f (I \otimes H)$
- 3b. Appy inversion of the mean: $-I + 2A$
Measure Qubits

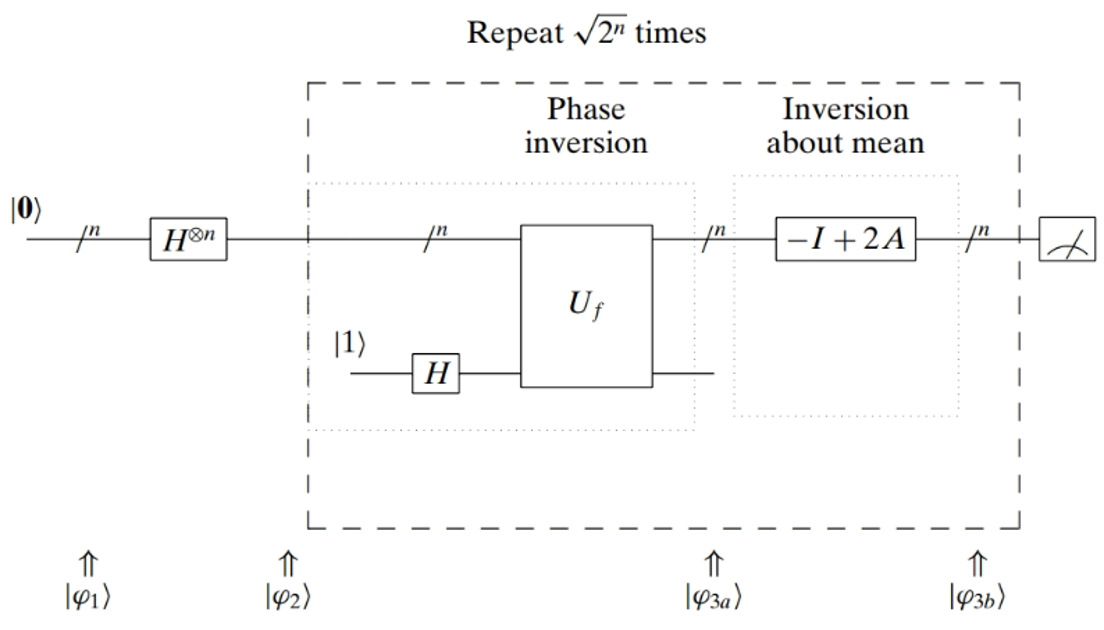
Quantum Circut

Superposition: Grover's algorithm starts by putting the quantum computer into a superposition state, representing all possible combinations of the database items simultaneously.
Oracles: An "oracle" is a quantum operation that marks the target item in the superposition of states. It flips the sign of the amplitude corresponding to the target item, effectively marking it.
Amplitude Amplification: The heart of Grover's algorithm lies in the amplitude amplification process, where the quantum state is iteratively modified to increase the amplitude of the target item and decrease the amplitudes of other non-target items.
Grover Operator: The Grover operator is a combination of the oracle and a transformation called the "diffusion operator," which amplifies the amplitude of the target state

Toffoli Gates

The Toffoli gate, also known as the CCNOT gate, is a fundamental reversible quantum logic gate with three input qubits. It performs a controlled-controlled-not operation, meaning that it flips the target qubit if and only if both control qubits are in the state $|1 \rangle$ . The Toffoli gate can be represented by the following matrix:

\text{Toffoli Gate: } |a, b, c\rangle \rightarrow |a, b, c \oplus (a \land b)\rangle

he Toffoli gate, being a controlled-controlled-not gate, can be used to implement this phase inversion and act as the Oracle in Grover's algorithm when appropriately combined with other quantum gates. Although the Toffoli gate is an important component in constructing the Oracle and Grover diffusion operator, its implementation can be challenging in certain physical quantum computing architectures. The reason is that the Toffoli gate requires three-qubit interactions, which can be more susceptible to noise and errors than two-qubit gates

Number of Iterations

The number of iterations required by Grover's algorithm to find the target item is approximately $\sqrt{N}$ . So, the total number of queries made is proportional to $\sqrt{N}$ , which is significantly faster than the classical $N/2$ queries.

Measuring the Result

After a certain number of iterations (approximately $\sqrt{N}$ ), a measurement is performed on the quantum state, collapsing it to one of the possible states. The probability of measuring the target item is high, increasing the chances of finding the correct answer.

Mean Inversion

Mean inversion is a fundamental step in Grover's algorithm that helps concentrate the amplitudes of the marked (target) item and disperse the amplitudes of the unmarked items. This step is performed using an operation called the "diffusion operator" or "mean inversion operator." The mean inversion operator can be understood as follows:

First, it calculates the average amplitude of all items in the superposition. Then, it reflects each amplitude around the average, effectively amplifying the amplitudes of items that were initially below the average and reducing the amplitudes of items that were above the average. Mathematically, if $|s \rangle$ represents the uniform superposition of all possible states and $N$ is the total number of states (items in the database), then the mean inversion operator, denoted by $D$ , is defined as:

D = 2A - I or\ D = -I + 2A

where $A$ is the outer product of the uniform superposition with itself, and I is the identity matrix. The factor of 2 ensures proper amplitude scaling during the inversion.

# Mean Inversion
m_inversion = QuantumCircuit(n + 1)
m_inversion.name = "MeanInversion"
m_inversion.to_gate()
 
for i in range(n):
    m_inversion.h(i)
    m_inversion.x(i)
 
# m_inversion.barrier()
 
m_inversion.h(3)
 
m_inversion.ccx(0, 1, 4)
 
m_inversion.ccx(2, 4, 3)
 
m_inversion.ccx(0, 1, 4)
 
m_inversion.h(3)
 
# m_inversion.barrier()
 
for i in range(n):
    m_inversion.x(i)
    m_inversion.h(i)
 
# m_inversion.barrier()
 
m_inversion.to_gate()

Mean inversion is applied to the quantum state after the oracle operation, effectively "diffusing" the amplitudes and causing constructive interference at the marked item.

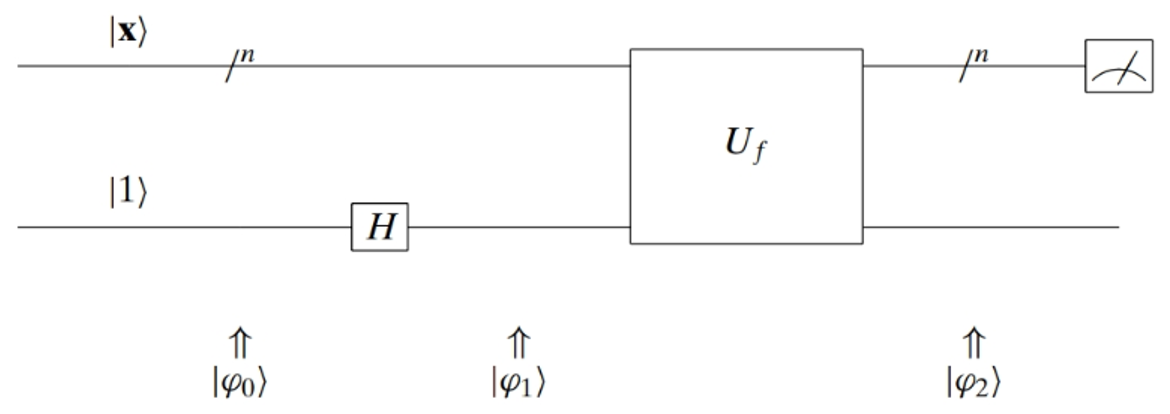
Phase Inversion

Phase inversion, also known as the "oracle," is the quantum operation that marks the target item in the superposition of states. It is a critical component of Grover's algorithm because it introduces a negative phase to the amplitude of the target item. The oracle operation can be represented by a unitary matrix $U_i$ , where the subscript " $i$ " denotes the index of the target item. When applied to the quantum state $| \psi \rangle$ , the oracle changes the sign of the amplitude corresponding to the target item:

$U_i | \psi \rangle = | \psi \rangle$ for all states | \psi \rangle except the target item, where

$U_i | \text{target} \rangle = -| \text{target} \rangle$

In other words, the oracle operation flips the sign of the amplitude of the target state, effectively marking it so that it can be identified later during the measurement process.

# Phase Inversion
p_inversion = QuantumCircuit(n + 1)
p_inversion.name = "PhaseInversion"
p_inversion.to_gate()
 
for i in range(n):
    if i == 1 or i == 2:
        p_inversion.x(i)
 
# p_inversion.barrier()
 
p_inversion.h(3)
 
# p_inversion.barrier()
 
p_inversion.ccx(0, 1, 4)
 
p_inversion.ccx(2, 4, 3)
 
p_inversion.ccx(0, 1, 4)
 
p_inversion.barrier()
 
p_inversion.h(3)
 
# p_inversion.barrier()
    
for i in range(n):
    if i == 1 or i == 2:
        p_inversion.x(i)

Together, mean inversion and phase inversion are iteratively applied in Grover's algorithm. These two operations play a pivotal role in concentrating the amplitude at the target item, leading to an increased probability of measuring the target state when the algorithm is executed. The algorithm requires approximately $\sqrt{N}$ iterations of these operations to find the target item with a high probability, providing the quadratic speedup compared to classical search algorithms.

Measuring the Result

 
# add oracles
for i in range(r):
    grovers.compose(p_inversion, range(n))
    grovers.compose(m_inversion, range(n))
 
# --------- run simulation ---------
for i in range(n):
    grovers.measure(i, i)
 
quasm_sim = Aer.get_backend('qasm_simulator')
shots = 1024
qobj = assemble(grovers, quasm_sim)
result = quasm_sim.run(qobj).result()
answer = result.get_counts()
plot_histogram(answer)
 
# Draw a circuts for Grovers Algorithm and Mean Inversion
m_inversion.draw(output='mpl', filename="MEAN_INVERSION.png")
grovers.draw(output='mpl', filename="Grovers.png")

Final Circut:

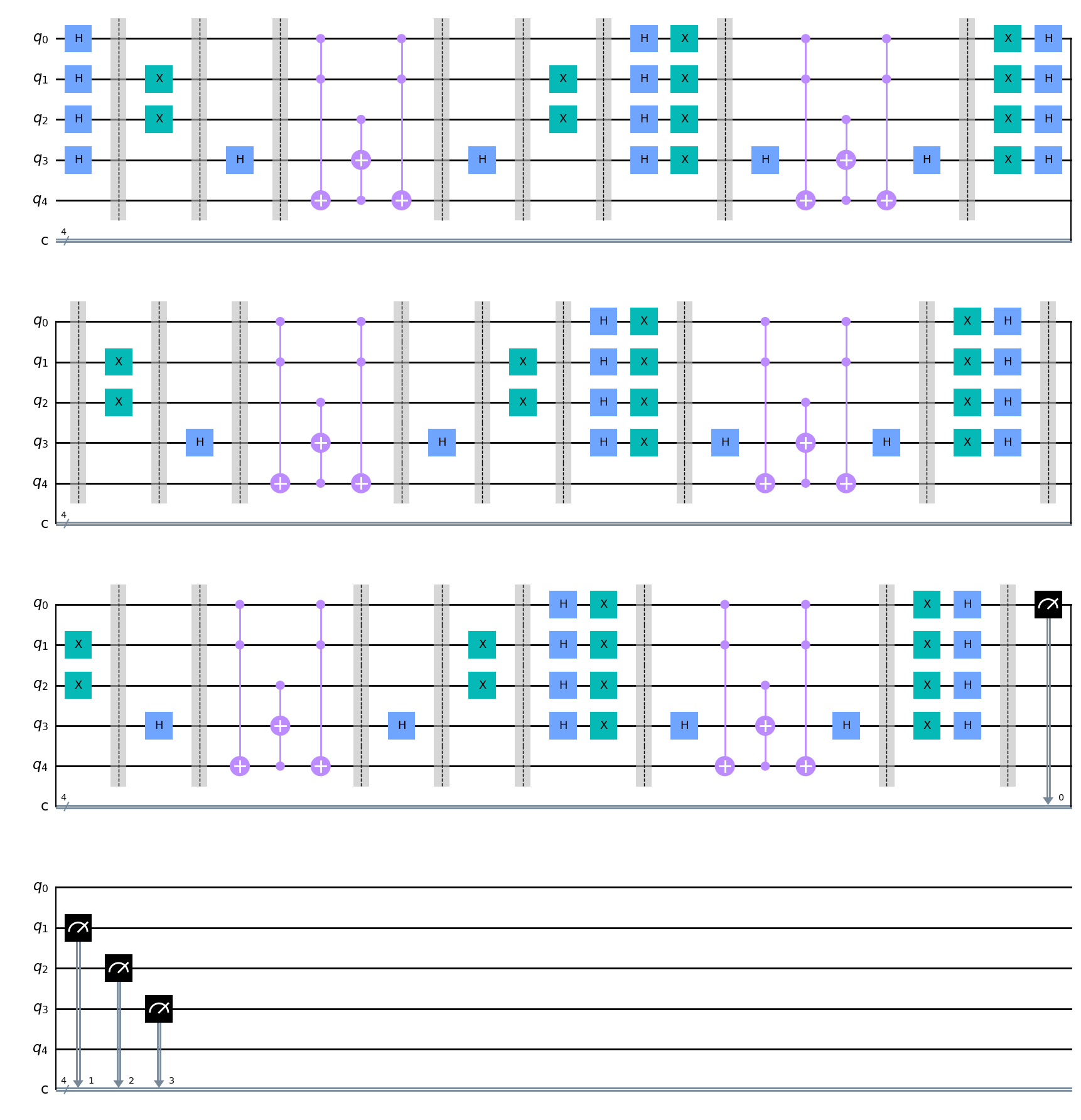
Limitations

It's essential to note that Grover's algorithm doesn't provide an exponential speedup like some other quantum algorithms. It's still limited by the $\sqrt{N}$ factor. Moreover, Grover's algorithm requires knowledge of the number of items in the database, which means it's not suited for problems where the size of the database is unknown.

References

[C. Figgatt, D. Maslov et al. "Complete 3-Qubit Grover Search on a Programmable Quantum Computer." Nature, Springer Nature, https://doi.org/10.1038/s41467-017-01904-7. Accessed 29 January 2023.]